ЦЕПЬ МАРКОВА
(простая)
— последовательность испытаний,
в каждом из которых может произойти одно и только одно из k событии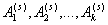 
и таких,
что условная вероятность
осуществиться событию 
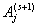в (s+1)-ом испытании (s = l,
2,
3...),
после того как в s-ом испытании произошло определенное событие,
зависит только от того,
каким было событие в s-ом испытании,
и не зависит от того,
какие события происходили в более ранних испытаниях: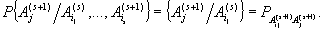 
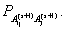— вероятности перехода из состояния 
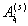в состояние 
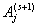; если они не зависят от s,
то цепь однородная. Множество вероятностей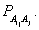 
за писываются в виде матрицы
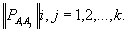Вероятности перехода за п шагов 
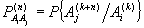удовлетворяют уравнению Маркова — Чемпена — Колмогорова: 
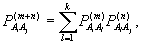где k—
число состояний.
Кроме простых Ц. М. рассматривают Ц. М. 2-го,
3-го и т. д. порядков,
когда вероятность осуществления события в данном испытании зависит от результатов 2,
3 и т. д. предыдущих испытаний. Рассматривается Ц. М. с непрерывным временем и конечным числом состояний.
В случае непрерывного времени и произвольного множества состояний имеем марковский процесс.
Последовательность слоев в разрезах флиша
,
последовательность эксплозий вулканов,
последовательность зерен в шлифах во многих случаях неотличимы от Ц.
М.,
что позволяет выяснить специфику процессов,
вызвавших появление соответствующих последовательностей (Вистелиус,
1966; Феллер,
1964). Г. С. Лелъчук,
М. Г. Романова.
|
